Forme indéterminée
2 مشترك
صفحة 1 من اصل 1
 Forme indéterminée
Forme indéterminée
Lorsqu'on cherche la limite d'une somme, d'un produit... de fonctions, des théorèmes algébriques nous renseignent parfois. Par exemple, si f tend vers 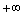 en
en 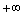 , et si g tend vers une limite finie l toujours en
, et si g tend vers une limite finie l toujours en 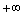 , alors f+g tend vers
, alors f+g tend vers 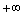 en
en 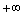 . Mais il existe des situations pour lesquelles ces théorèmes ne s'appliquent pas, et où tout est possible :
. Mais il existe des situations pour lesquelles ces théorèmes ne s'appliquent pas, et où tout est possible :
De telles situations sont appelées formes indéterminées. Parvenir tout de même à trouver la limite, c'est lever l'indéterminé.
***
Dicomaths
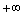 en
en 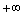 , et si g tend vers une limite finie l toujours en
, et si g tend vers une limite finie l toujours en 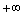 , alors f+g tend vers
, alors f+g tend vers 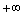 en
en 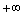 . Mais il existe des situations pour lesquelles ces théorèmes ne s'appliquent pas, et où tout est possible :
. Mais il existe des situations pour lesquelles ces théorèmes ne s'appliquent pas, et où tout est possible : - le quotient de deux fonctions tendant toutes les deux vers l'infini, ou vers 0.
- le produit de deux fonctions tendant l'une vers l'infini, l'autre vers 0.
- la différence de deux fonctions tendant vers le même infini.
De telles situations sont appelées formes indéterminées. Parvenir tout de même à trouver la limite, c'est lever l'indéterminé.
***
Dicomaths

Mohamed- مدير موقع العلوم الرياضية

-
 عدد الرسائل : 1265
عدد الرسائل : 1265
العمر : 35
Localisation : Paris
Emploi : etudiant en Classes Preparatoires aux Grandes Ecoles PCSI Lycee technique Raspail Paris
Loisirs : Internet Programmation Electronique
تاريخ التسجيل : 04/04/2007
بطاقة الشخصية
ملاحظات: -

 رد: Forme indéterminée
رد: Forme indéterminée
merci mohamed
je px ajouter que pour lever l'indeterminé on utilise des techniques comme le conjugué la factorisation par x² à l'intérieur de la racine
...........
je px ajouter que pour lever l'indeterminé on utilise des techniques comme le conjugué la factorisation par x² à l'intérieur de la racine
...........
ilham- نائب مشرف

-
 عدد الرسائل : 356
عدد الرسائل : 356
العمر : 33
Localisation : Agadir MOROCCO
Emploi : Terminale Sciences Maths
Loisirs : surfer sur le net
تاريخ التسجيل : 01/09/2007
بطاقة الشخصية
ملاحظات: -

 رد: Forme indéterminée
رد: Forme indéterminée
oui bien sur dans cette cas on utilise tous les techniques de mathematiques qu'on sait pour resoudre le probleme

Mohamed- مدير موقع العلوم الرياضية

-
 عدد الرسائل : 1265
عدد الرسائل : 1265
العمر : 35
Localisation : Paris
Emploi : etudiant en Classes Preparatoires aux Grandes Ecoles PCSI Lycee technique Raspail Paris
Loisirs : Internet Programmation Electronique
تاريخ التسجيل : 04/04/2007
بطاقة الشخصية
ملاحظات: -

صفحة 1 من اصل 1
صلاحيات هذا المنتدى:
لاتستطيع الرد على المواضيع في هذا المنتدى